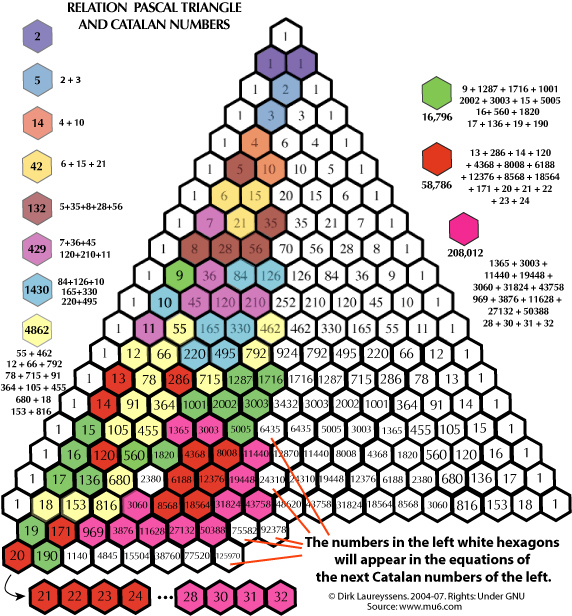
CATALAN NUMBERS. You can see in next Pascal Triangle that each Catalan number is the sum of specific Pascal numbers. The Catalan numbers occupy all Pascal numbers except the middle row and the rows of ones.
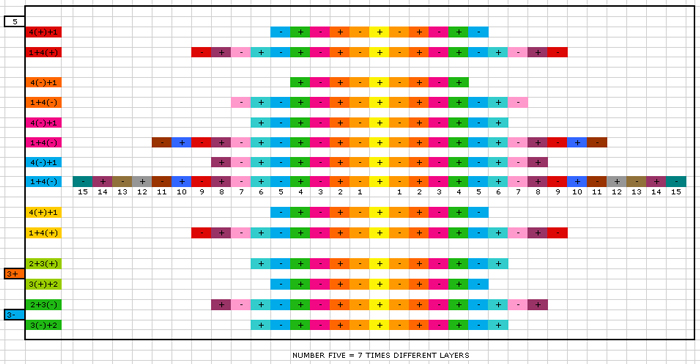
This image shows 14 geometric combinations of spacetime layers on the fifth level. There are 7 types qua number of layers (but each has another history). We can't just say that they are identical, even if the have an identical number of layers. For example the first 5 [4(+)+1] is not identical to the 12th 5 [3(+)+2] due the other parents, although both count 5 layers on each side. Next image (click on to download the pdf) shows how the direction of a pelastration (membrane penetration) creates other membrane combinations in holons. 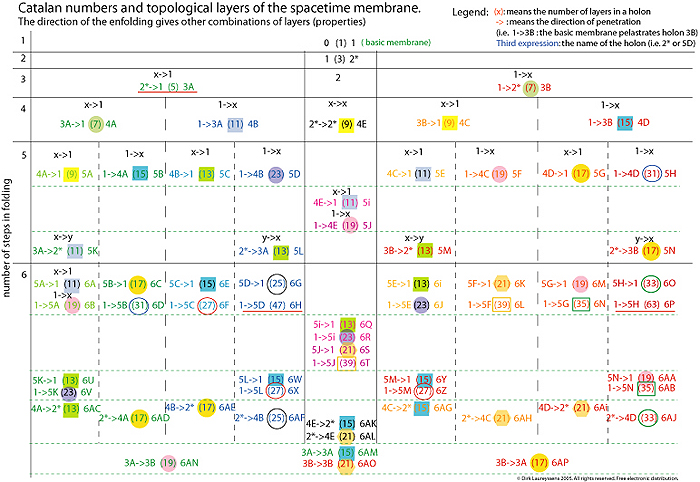 |
|||||||||
|
Next animated image shows in a dynamic way the first four steps of the growth of numbers (holons).
|
|||||||||
 |
|||||||||
|
© Dirk Laureyssens, 2004. All rights reserved.
|