|
|
|
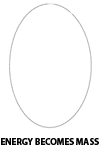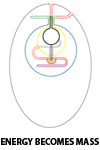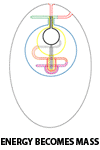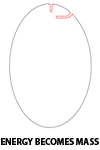
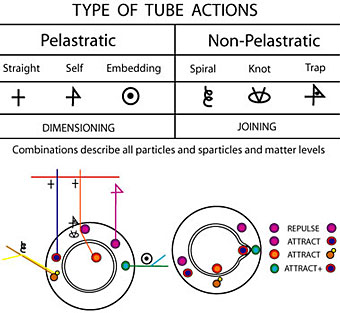
Pelastration (3)
Tubes can have several ways to connect with each other: by pelastration (two independent tubes, self-pelastration by a single tube, embedding into another tube), and non-pelastratic ways (spiraling of one tube around another, making a knot around or with another tube, a tube trapped in a self-pelastration curl).
The foam of space is then a giant space of inter-combinations from which parts and subparts are 'isolated' from the rest by the pelastration manifold (a 'wormhole'. Pelastrated zones in space are sub-spaces with higher compressed energies and with a own time-scale . (cfr. Smolin/M-Theory with the Baby-universes and the Einstein-Rosen-Bridges).
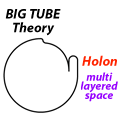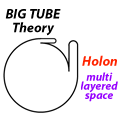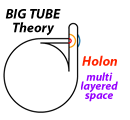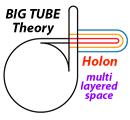
The straight pelastration and the embedding pelastration are relative simple combinations since two different kind of space conditions are joined, but a self-pelastration is only possible if specific parameters are valid (e.g. pressure balance inside must been overcome, sharp curvation, correct impact angle, etc.). For example a previous twist of the tube, or a previous non-pelastrational joint (spiral, knot or trap) with or by another tube can draw a part of the tube through its own body.
|
|
 |
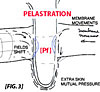
When we analyze the pelastration models we need to understand that around the impact zone there is a zone of changed resonance. Interferences and Landau Level-gaps will happen. This will bring harmonic or inharmonic frequencies combinations and also fluxtuations (due pressure variations in wormhole zone and valve [P-factor]. After the pelastration the extra-dimensioned tube has other properties of vibration (depending the kind of tubes that pelastrates). The zone of the manifold node or joint becomes thus for other tubes an uncertainty or neutral zone, except when approached from the correct angle(s), lets call it a 'slot-trajectory'. This may explain a number of node or vertex related phenomena found in "Platonic solids" (Sacred geometry) and also seen in music (Diatonic sound ratio's). This 'angles' of acceptance may explain the 'symmetry' in various aspect of physics (e.g. rotation and still keep the same inter-position).
|
|